
Sistema diédrico > Representación en SDO > El punto
Representación del punto
Introducción.
Antes de comenzar, recordamos que cualquier figura tridimensional se compone por un conjunto de planos que se cortan entre si, formando segmentos (aristas) que a su vez se cortan entre si, determinando una serie de puntos (vertices).
Por tanto, podemos decir sin posibilidad de error que toda figura tridimensional esta formada por un conjunto de puntos. Por esta razón, debemos prestar especial atención a este capítulo.
Representación.
¿Cómo se representaba un punto A en el espacio? ¿Y cómo lo representamos en el sistema diédrico?
Efectivamente, para poder representar un punto A, necesitamos sus proyecciones ortogonales: puntos-trazas sobre los planos de proyección: Horizontal y Vertical.
Pero, ¿Por qué son necesarias como minimo dos proyecciones, no sería suficiente una de sus dos proyecciones?
Para responder a esta pregunta, observa la siguiente ilustración respondiendo a las siguientes cuestiones:

Si solo tuvieramos una proyección, por ejemplo la Horizontal, ¿Se podria diferenciar el punto A1 y el punto A, de alguna manera?.
Y si solo consideramos la proyección vertical, ¿Qué pasaria con los puntos A y A2?
Como observamos, las proyecciones de todos los puntos contenidos en una recta imaginaria AA1, perpendicular al PH, tendrian sus proyecciones horizontales coincidentes en A'. Igual sucedería con el cualquier punto situado en la recta imaginaria AA2.
Por tanto, son necesarias siempre, como minimo, las dos proyecciones de cualquier elemento en el espacio, ya sea punto, recta o plano.
De esta manera, cualquier punto A en el espacio, se representa en el sistema diédrico por sus dos puntos-trazas: A(A', A''). Y gracias a la caracteristica fundamental del sistema, la reversibilidad, que nos permite:
-
Si conocemos las proyecciones (a,a') de un punto A, situarlo en el espacio.
Bastaría con dibujar por esas proyecciones dos perpendiculares al PV y PH, respectivamente.
-
Si conocemos el punto A (representación tridimensional o perspectiva), situar sus proyecciones (a, a') .
Trazamos lineas de referencia perpendiculares por el punto A al PV y PH, obteniendo sus proyecciones en los cortes con los planos.
*Las perpendiculares trazadas se conocen como líneas de referencia.
Esta propiedad de reversibiliidad del sistema creado por Monge, también permite trasladar culalquier representación tridimensional (perpectivas) a las dos dimensiones del papel. Para ello, simplemente abatimos o giramos, alrededor de la LT (=------=), el plano horizontal sobre el plano vertical. De tal forma, que las proyecciones a'' y a' del punto se encuentran unidos por una linea de referencia perpendicular a la LT. (ver animación)
A(YA,ZA)
La tercera proyección.
En el sistema diédrico existe una indeterminación en cuanto a las proyecciones de elementos contenidos en planos de perfil, es decir, existen confusiones a la hora de representar los elementos contenidos en estos planos. Para poder salvar esa indeterminación, es necesario utilizar una tercera proyección sobre un plano de perfil, que es perpendicular a los dos planos, y por tanto a la LT.
La tercera proyección del punto A sobre el plano de perfil (PP), es el punto a’’. Este plano se abate o gira, en sentido anti-horario, sobre el vertical de proyección, quedando definido el PP por una recta perpendicular a LT (traza del PP).
Así, cualquier punto situado en el espacio, es fácilmente ubicado mediante las coordenadas cartesianas del punto, referidas al triedo de ejes trirectángulo con origen en el punto O (origen de coordenadas):
A(XA,YA,ZA)

*como regla nemotecnica para recordar el orden de estas coordenadas, empleamos la palabra REFALCO, es decir, REFerenciaALejamientoCOta.
*como regla nemotecnica para recordar el orden de estas coordenadas, empleamos la palabra DESALCO, es decir, DESplazamientoALejamientoCOta.
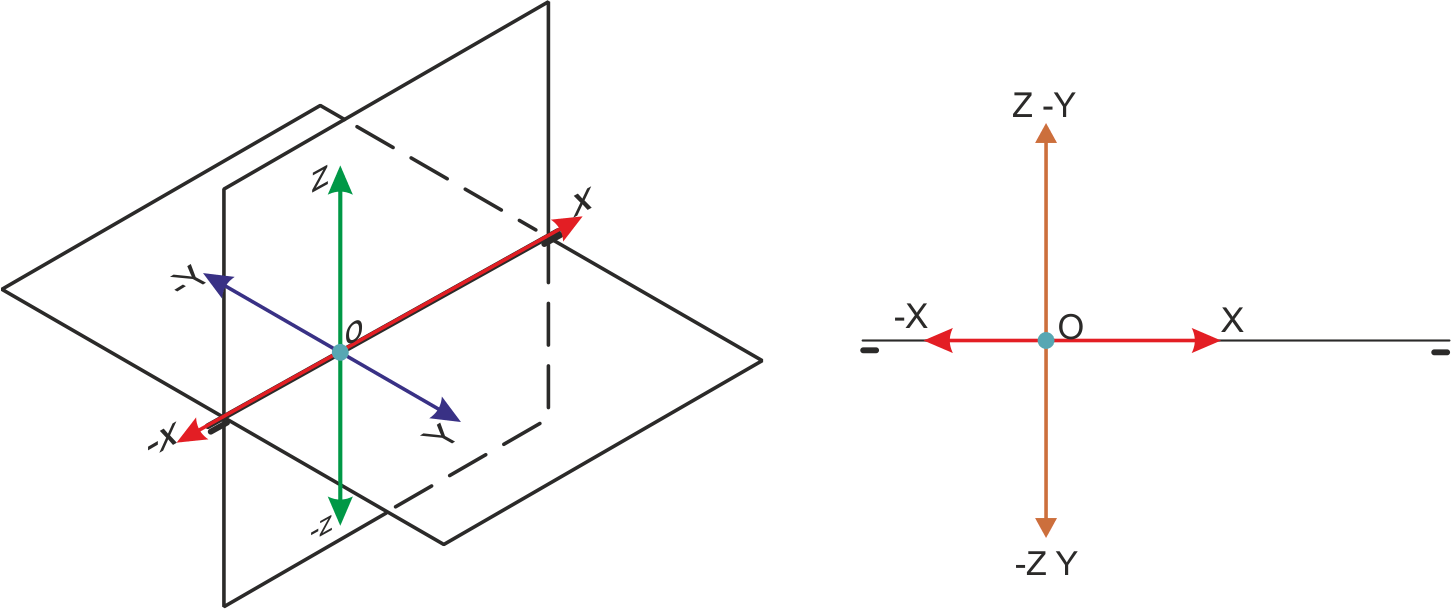
El desplazamiento o referencia (XA) de un punto es:
La distancia entre un Punto en el espacio y el Plano de perfil(PP), es decir, la distancia que hay desde sus proyecciones vertical y/o horizontal a la traza del plano de perfil.
Nota:
Los puntos situados en el 1º o 4º diedro tienen desplazamiento positivo, se sitúan a la derecha de la traza del plano de perfil.
Los puntos situados en el 2º o 3º diedro tienen desplazamiento negativo, es decir, sus proyecciones se sitúan a la izquierda de la traza.
El alejamiento (YA) de un punto es:
la distancia de este punto al plano vertical, o la distancia entre su proyección horizontal y la LT.
Nota:
El alejamiento es positivo si el punto está por delante del PV, es decir en 1º o 4º cuadrante.
El alejamiento es negativo si el punto se se sitúa por detrás del PV, es decir en el 2º o 3º diedro
El alejamiento es nulo si el punto se encuentra en el PV.
La cota (ZA) de un punto es:
la distancia de este punto al plano horizontal, es decir, la distancia entre su proyección vertical y la LT.
Nota:
La cota es positiva si el punto está por encima del horizontal, es decir en el 1º o 2º diedro.
La cota es nula si el punto está en el PH.
La cota es negativa si el punto se sitúa por debajo del PH, es decir, en el 3º o 4º diedro.
Alfabeto del punto.
Se denomina alfabeto del punto, a las diversas posiciones que puede ocupar un punto en el espacio respecto a los planos de proyección y a los bisectores, así como a las proyecciones que le corresponden en cada caso. Estas posiciones son 17.
Puntos situados en los octantes.
8 posiciones.
Cuando no pertenecen ni en los planos de proyección ni a los bisectores, se encontrarán en los octantes (los planos bisectores dividen cada diedro en dos octantes)
Tendrán siempre sus cotas y alejamientos desiguales, siendo indistintamente una positiva y otra negativa, ambas positivas, o ambas negativas, según el cuadrante al que pertenezca.
Resumiendo:
Los puntos del 1º diedro (1º & 2º octante), tienen una proyección a cada lado de LT, la horizontal por debajo y la vertical por encima.
Los puntos del 3º diedro (5º & 6º octante) como los del primero, tienen sus proyecciones a cada lado del LT, pero invertidas, es decir, la horizontal por encima y la vertical por debajo.
Los puntos del 2º diedro (3º & 4º octante) tienen sus dos proyecciones por encima de LT,
Los puntos del 4º diedro (7º & 8º octante) tiene las dos por debajo de LT.
Puntos situados en los planos bisectores. 4 posiciones.
Todo punto situado en un plano bisector, equidista de los planos de proyección del diédro correspondiente. Según esto, sus proyecciones serán equidistantes a la LT, misma cota y alejamiento. Podemos encontrarnos las siguientes situaciones:
-
Si un punto pertenece al 1º bisector, sus proyecciones se situá equidistantes a ambos lados de la LT, y por tanto, su cota y alejamiento serán iguales, y el punto pertenece al 1º o al 3º diédro
-
Si un punto en el 2º bisector sus proyecciones se confunden al tener valores absolutos iguales, y el punto pertenece al 2º o al 4º diedro.
Puntos situados en los planos de proyección. 5 posiciones.
Se caracterizan en que el punto en el espacio se confunde con su punto-traza del plano de proyeccion que contiene al punto, la otra proyección está contenida siempre en la LT.
Dependiendo de en que semiplano se situé el punto, existen 4 posiciones, que poseen esta característica.
A estas posiciones le sumamos los puntos pertenecientes a la LT, que pertenecen a ambos planos de proyección y, también, a ambos bisectores, por lo que tienen sus proyecciones confundidas.
Mover las proyecciones (rombos) del punto A (a,a') para visualizar las distintas posiciones del punto en el espacio, segun las indicaciones del alfabeto del punto.
Animación resumen de las distintas Posiciones del punto, con sus características ( + ). Puedes introducir las coordenadas de un punto para comprobar su situación. En Evaluación puedes comprobar tu nivel de conocimiento.
Unidad Sistema diédrico de José Antonio Cuadrado.
AcTICvidades & Recursos
El Punto y sus diferentes posiciones (aplicación interactiva) Muy útil para entender y explicar el fundamento del sistema diédrico y la relación entre las proyecciones de un punto y su posición en el espacio. (Autores: Mª Ángeles Velázquez Pérez y Fernando Ortiz de Lejarazu)
El Punto y sus diferentes posiciones: Presentación en power point, para ayudar en la explicación en el aula.
(Autores: Mª Ángeles Velázquez Pérez y Fernando Ortiz de Lejarazu)
Cuestionario realizado con el programa Hot-Potatoes para practicar el reconocimiento de las diferentes posiciones del punto respecto a los planos de proyección. Muestra 10 preguntas seleccionadas aleatoriamente entre 20, por lo que es diferente cada vez que se carga.
(Autores: Mª Ángeles Velázquez Pérez y Fernando Ortiz de Lejarazu)
Versión con formulario para introducir los datos personales y enviar los resultados al profesor.



